Figure 1. Principle of random conical tilting, showing how many rotated images within a cone come together to form a surface. Radermacher et al. (1987)
Simple Electron Microscopy Primer
In the previous sections, we discussed how experimental particles are picked, aligned, and classified. In this section, we will briefly explain the two methods most commonly used for generating a three-dimensional model via single particle reconstruction.
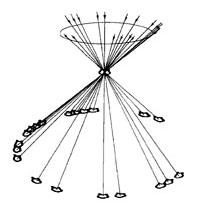
For a specific class of particles, once the untilted particles are aligned with each other, those angles and shifts are applied to the tilted pairs to determine their relative orientations in space. As seen in Figure 1, the projections of these aligned particles will form a cone with a fixed angle (the tilt angle) and a random azimuths (rotation) around the cone, matching the in-plane angles found in the alignment of the untilted particles.
Another reconstruction method searches for the intersection of any two projections in Fourier space. The Fourier transform of the experimental projections all form slices around a common core in Fourier space. Therefore, the intersection of these projections are unique (unless the projections perfectly overlap), and their relative orientation can be found when three or more projections are used. A principal problem with this method is that the handedness of the image is lost. This, however, can later be corrected by visual examination of the model with other known structural information.
There are several other methods that can be used for generating three-dimensional models from data acquired by EM. They include:
Helical reconstruction is used when the protein of interest forms a natural helix. Since the helix is a recurring structure with a very well defined pattern, the repeating pattern of the helix can be exploited to solve the structure. In this case, no alignment of the particles is needed, since the individual positions of subunits within the helix are clearly defined by the shape of the helix. Two common examples of structures solved by helical reconstruction are TMV and microtubules.
Icosahedral reconstructions also take advantage of internal symmetry and repetition to generate a detailed three-dimensional structure from the data set. In this case, the symmetry is icosahedral (twenty-one sided). Many viruses exhibit icosahedral symmetry in their capsid proteins, and this method has been used to solve their structures.
Electron crystallography is similar to x-ray crystallography in that it exploits the repeating pattern found within a crystal to generate a structure. Just as with x-ray crystallography, difraction patterns are generated and are used to define an electron density map. However, it differs in that the crystal used is a two-dimensional sheet as opposed to three three-dimensional crystals of x-ray crystallography.
However, these methods do not generally deal with single particles, but rather with repeating arrays of particles. Therefore, no further mention will be made of them here.